확률 개념 설명 : 소개

이 문서는 영문으로된 내용을 카카오 번역기를 활용하여 번역한 내용입니다. 
개인적인 공부 및 추후 다시 볼 수 있도록 하기 위해 개인 블로그에 번역 내용을 옮겨 놓았습니다.
원문과 내용이 다를시 책임지지 않으며, 저작권 문제가 발생시 언제든 삭제 될 수 있습니다. 

원문보기 : https://towardsdatascience.com/probability-concepts-explained-introduction-a7c0316de465

확률 개념 설명 : 소개

나는 여러 해 동안 확률 이론의 여러 측면에 관한 많은 텍스트와 기사를 읽었으며, 각각의 지식은 무슨 일이 일어나고 있는지 이해하기 위해 필요한 수준의 다른 지식을 필요로하는 것처럼 보입니다. 나는 결코 이 분야의 전문가는 아니지만 다양한 개념을 설명할 수 있는 일련의 접근 가능한 기사가 되기를 바라는 것을 작성함으로써 기여할 수 있다고 느꼈습니다. 이것은 시리즈의 첫 번째이며 몇 가지 기본 정의에 대한 소개가 될 것입니다.

정의와 표기법

확률은 적어도 하나의 사건과 관련이 있는 경우가 많습니다. 장난감 예제로 주사위를 굴리거나 가방에서 컬러 볼을 꺼내는 것이 포함됩니다. 이 예에서 사건의 결과는 무작위적이므로 (주사위를 굴릴 때 주사위가 표시할 값을 확신할 수 없음) 이러한 이벤트의 결과를 나타내는 변수를 임의의 변수(종종 RV로 약칭 함)라고합니다.

우리는 종종 확률 변수가 특정 값을 취할 확률을 아는 데 관심이 있습니다. 예를 들어, 내가 공정한 6면 주사위를 굴릴 때 3이 나올 확률은 얼마나 될까요? 여기서 ‘공정’이라는 단어는 여섯 개의 면 중 하나가 나올 확률이 1, 2, 3, 4, 5, 6이라는 것을 알려주기 때문에 중요합니다. 직관적으로, 대답은 1/6이라고 말할 수 있겠죠. 맞습니다! 하지만 수학적으로 어떻게 쓸 수 있을까요? 우선, 여기서 임의의 변수가 주사위를 굴리는 것과 관련된 사건의 결과라는 것을 이해해야 합니다. 일반적으로 임의의 변수는 대문자로 표시됩니다. 여기서 우리는 X로 표시합니다. 그러므로 우리는 X=3 일 확률이 무엇인지 알고 싶습니다. 하지만 수학자들이 글을 쓸 때 게으르기 때문에 ‘확률이 얼마나 되느냐?’고 묻는 속기는 P라는 글자를 사용하는 것이다. 그러므로 우리는 "내가 공정한 6면 주사위를 굴릴 때 3나올 확률은 얼마나 될까?"를 수학적으로 표시하면 "P(X=3)" 입니다.

세 가지 유형의 확률

위의 것은 확률 변수의 개념과 확률에 대한 표기법을 소개했습니다. 하지만 확률은 상당히 복잡해질 수 있습니다. 아마도 가장 먼저 이해해야 할 것은 다른 유형의 확률이 있다는 것입니다. 그것은 한계, 결합 또는 조건부일 수 있습니다.

한계 확률: A가 이벤트라면 한계 확률은 해당 이벤트가 발생할 확률 인 P(A)입니다. 예 : 우리가 전통적인 카드 팩을 가지고 있다고 가정하면, 한계 확률의 예는 팩에서 가져온 카드가 빨간색일 확률입니다 : P(빨간색) = 0.5.

결합 확률: 둘 이상의 이벤트가 결합할 확률입니다. 시각적으로 그것은 Venn Diagram (아래 그림 참조)에서 두 이벤트의 원이 교차하는 것입니다. A와 B가 두 개의 이벤트라면 두 이벤트의 결합 확률은 P(A ∩ B)로 작성됩니다. 예 : 팩에서 가져온 카드가 빨간색이고 값 4가 P(빨간색 및 4) = 2/52 = 1/26 일 확률. (전통적인 카드 한 팩에는 52 장의 카드가 있으며, 2 장의 빨간색 카드는 하트와 다이아몬드입니다). 이 예제는 나중에 자세히 살펴보겠습니다.

조건부 확률: 조건부 확률은 다른 사건이 이미 발생했다는 것을 알면 어떤 사건 (들)이 발생할 확률입니다. A와 B가 두 개의 이벤트라면 B가 발생했을 때 발생하는 A의 조건부 확률은 P (A|B)로 기록됩니다. 예 : 빨간색 카드를 그렸다는 점을 감안할 때 카드가 4일 확률은 P (4|red) = 2/26 = 1/13입니다. (팩에는 52 장의 카드가 있고, 26 장은 빨간색이고 26 장은 검은 색입니다. 이미 빨간색 카드를 골랐기 때문에, 우리는 선택할 카드가 26장 밖에 없다는 것을 알고 있습니다.

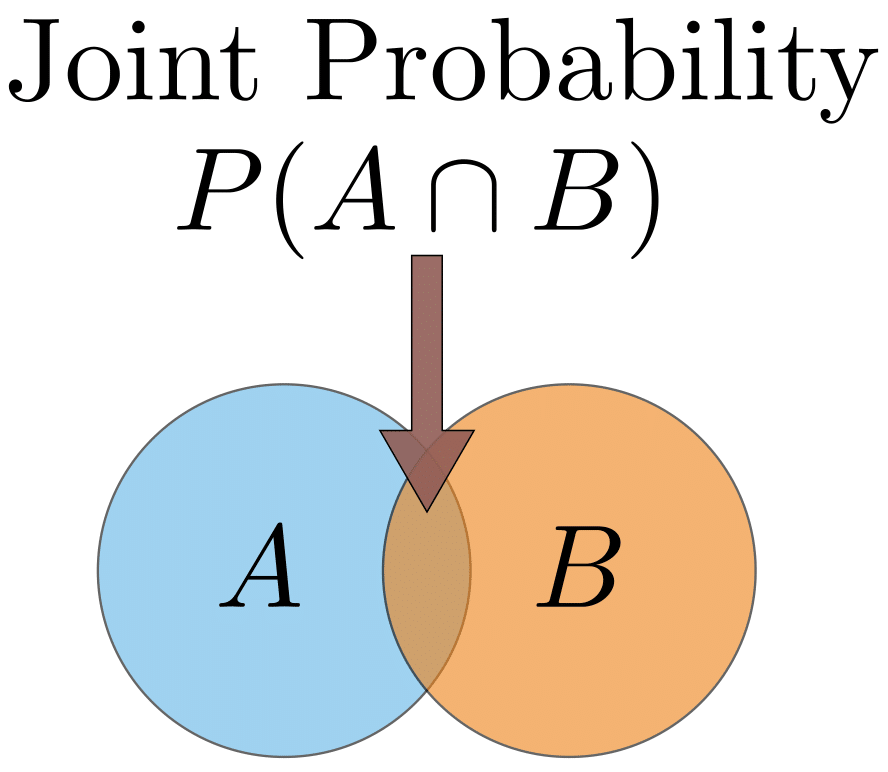
벤 다이어그램은 두 사건 A와 B의 결과의 ‘공간’을 보여준다. 다이어그램에서 두 이벤트가 겹칩니다.이 겹침은 결합 확률, 즉. 이벤트 A와 이벤트 B가 모두 발생할 확률입니다. 이벤트 사이에 중첩이 없으면 결합 확률은 0이됩니다.

확률 유형 연결: 일반 곱셈 규칙

일반적인 곱셈 규칙은 세 가지 유형의 확률을 모두 연결하는 아름다운 방정식입니다.

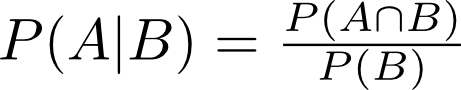
예제에 대한 자세한 설명

때로는 결합 확률과 조건부 확률을 구별하는 것이 매우 혼란 스러울 수 있으므로 카드 게임에서 카드를 선택하는 예를 사용하여 그 차이를 알아 보겠습니다.

빨간색과 4인 카드를 뽑을 확률을 찾고자 하는 경우, 즉 결합 확률 P(빨간색과 4). 52 장의 카드를 모두 뒤집어 무작위로 뽑는 것을 상상해보세요. 52 장의 카드 중 2 장은 빨간색과 4 (다이아몬드 4, 하트 4)입니다. 그래서 결합 확률은 2/52 = 1/26입니다.

우리가 카드를 선택할 확률을 찾고자하는 경우, 카드가 이미 빨간색이라는 것을 알면 4라는 카드를 뽑을 확률, 즉 조건부 확률 P(4|빨간색)를 찾으려면 52 장의 카드를 모두 가지고 있다고 상상해보세요. 그러나 카드를 무작위로 선택하기 전에 카드를 정렬하고 26 개의 빨간색 카드를 모두 선택합니다. 이제 26장의 카드를 아래로 향하게 하고 무작위로 카드를 고르세요. 다시 말하지만, 빨간색 카드 중 2개가 4이므로 조건부 확률은 2/26 = 1/13입니다.

또는 수학을 선호한다면 위에서 정의한 일반 곱셈 규칙을 사용하여 결합 확률을 계산할 수 있습니다. 먼저 방정식의 주제인 P(A ∩ B)의 결합 확률을 재 배열합니다 (즉, P(A ∩ B)를 등호의 왼쪽에 놓고 다른 모든 것을 오른쪽에 놓으십시오). 재배치 후 P(A ∩ B) = P(A | B) ✕ P(B)를 얻습니다. 카드가 4인 이벤트를 A, 카드가 빨간색인 이벤트를 B라고 합시다. 위에서 말했듯이 P(A | B) = 1/13 및 P(B) = 1/2 (카드의 절반은 빨간색). 따라서 P(A ∩ B) = 1/13 ✕ 1/2 = 1/26.

확률 규칙 : '그리고'와 '또는'

‘그리고’ 규칙

우리는 이미 결합 확률로 위장한 ‘그리고’ 시나리오를 보았지만, ‘그리고’ 시나리오에서 확률을 계산하는 방법은 아직 알지 못합니다. 자, 예를 들어보죠. 우리에게 두 가지 사건이 있다고 가정 해 봅시다 : 이벤트 A - 공정한 동전 던지기, 이벤트 B - 공정한 주사위 굴림. 우리는 6을 굴릴 확률과 동전이 머리에 착륙할 확률을 아는 데 관심이 있을 수 있습니다. 따라서 6을 굴릴 수있는 확률과 동전이 머리에 착륙할 확률을 계산하기 위해 위의 일반 곱셈 규칙을 재배치하여 P(A ∩ B) = P(A | B) ✕ P(B) 를 얻을 수 있습니다. 우리는 사건 A가 동전을 던지고 B가 주사위를 굴리고 있다는 것을 알고 있습니다. 따라서 P(A|B) 용어는 “내가 주사위로 6을 굴렸다는 점을 감안할 때, 머리에 동전이 착륙할 확률은 얼마나 되는가?”라고 묻습니다. 이 사건은 독립적입니다. 이 시나리오에서 동전 던지기의 결과는 우리가 주사위에 무엇을 굴려도 동일합니다. 수학적으로 우리는 이것을 P(A | B) = P(A)로 표현합니다. 따라서 이벤트가 독립적 일 때, 결합 확률은 이벤트의 개별 한계 확률의 곱일뿐입니다 : P(A ∩ B) = P(A) ✕ P(B). 따라서 P(동전이 머리에 착륙 및 6) = P(A=머리, B=6) = 1/2 ✕ 1/6 = 1/12.

P(A=머리, B=6)를 썼습니다. 사건 사이의 쉼표는 결합 확률에 대한 속기입니다 (이를 문헌에서 볼 수 있습니다).

많은 현실 세계의 시나이로에서 사건은 실제로는 그렇지 않더라도 독립적이라고 가정해야 합니다. 이래야 수학이 훨씬 쉬워지기 때문입니다. 보너스는 종종 결과가 매우 유용하다는 것입니다. Naive Bayes의 방법은 아마도 데이터 과학에서 가장 일반적인 예일 수 있으며 일반적으로 텍스트 분류 문제에서 상당히 좋은 결과를 제공합니다.

‘또는’ 규칙

‘그리고’ 규칙을 가지고 우리는 개별 확률을 곱해야 했다. ‘또는’ 시나리오에 있을 때 우리는 개별 확률을 더하고 교차점을 빼야 한다. 수학적으로 우리는 이것을 P(A ∪ B) = P(A) + P(B) - P(A ∩ B)로 씁니다. 왜 우리가 이런 일을 해야 하는 걸까요? 위의 그림에서 벤 다이어그램으로 돌아갑니다. A에 대한 원과 B에 대한 원을 추가하면 교차점을 두 번 추가한다는 의미입니다. 그러므로 우리는 교차점을 빼야 합니다.

따라서 위의 예를 바꾸어 6번을 굴릴 확률이나 동전이 머리에 떨어질 확률을 찾아보면. 이것은 P(동전이 머리에 착륙 또는 6) = P(A=머리 ∪ B=6) = 1/2 + 1/6 - 1/12 = 6/12 + 2/12 - 1/12 = 7/12입니다.

∪ 기호는 '연합'으로 알려져 있으며 '또는'시나리오에서 사용됩니다.

교차점을 빼지 않아도 되는 경우도 있습니다. 벤 다이어그램의 두 원이 겹치지 않을 때 이런 현상이 발생합니다. 두 이벤트의 원이 겹치지 않을 때 우리는 이러한 이벤트가 상호 배타적이라고 말합니다. 이것은 교차가 0이라는 것을 의미 하며 P(A ∩ B) = 0으로 쓰여집니다. 이 경우를 다루는 예를 들어보겠습니다. 우리가 주사위를 굴려서 5 또는 6을 굴릴 확률을 알고 싶다고 가정 해 봅세요. 이 이벤트들은 상호 배타적입니다. 왜냐하면 나는 5와 6을 굴릴 수 없기 때문입니다. 따라서 벤 다이어그램의 원은 겹치지 않습니다. 따라서 5 또는 6을 굴릴 확률은 1/6 + 1/6 = 2/6 = 1/3입니다 (우리는 아무것도 빼지 않았습니다).

정리하며

여기까지 와줘서 감사합니다. 혹시라도, 당신이 아무것도 새로운 것을 배우지 못했다고 해도 내 글이 당신에게 접근할 수 있었으면 좋겠습니다. 만약 뭔가 불분명한 것이 있거나, 내가 몇 가지 실수를 저질렀다면, 의견을 남겨주세요. 이 시리즈의 다음 글에서 나는 좀 더 진보된 개념을 살펴볼 것입니다. 다음 글은 예제를 통해 최대 우도를 설명합니다.